In my last blog post I showed what to look out for when you build a GPU cluster. Most importantly, you want a fast network connection between your servers and using MPI in your programming will make things much easier than to use the options available in CUDA itself.
In this blog post I explain how to utilize such a cluster to parallelize neural networks in different ways and what the advantages and downfalls are for such algorithms. The two different algorithms are data and model parallelism. In this blog entry I will focus on data parallelism.
So what are these two? Data parallelism is when you use the same model for every thread, but feed it with different parts of the data; model parallelism is when you use the same data for every thread, but split the model among threads.
For neural networks this means that data parallelism uses the same weights and but different mini-batches in each thread; the gradients need to be synchronized, i.e. averaged, after each pass through a mini-batch.
Model parallelism splits the weights of the net equally among the threads and all threads work on a single mini-batch; here the generated output after each layer needs to be synchronized, i.e. stacked, to provide the input to the next layer.
Each method has its advantages and disadvantages which change from architecture to architecture. Let us look at data parallelism first and its bottlenecks first and in the next post I will look at model parallelism.
Severity of the network bottleneck of data parallelism
The idea of data parallelism is simple. If you have, say, 4 GPUs you split a mini-batch into parts for each of them, say, you split a mini-batch with 128 examples into 32 examples for each GPU. Then you feed the respective batch through the net and obtain gradients for each split of the mini-batch. You then use MPI to collect all the gradients and update the parameters with the overall average.
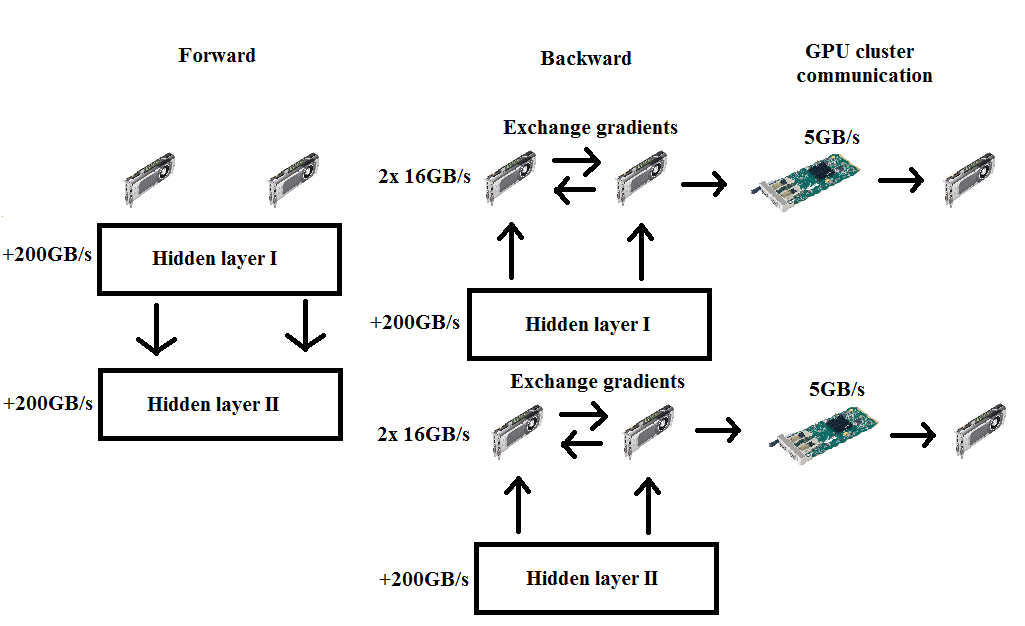
The biggest problem with this approach is that during the backward pass you have to pass the whole gradient to the all other GPUs. If you have a 1000×1000 weight matrix then you need to pass 4000000 bytes to each network. If we take a 40Gbit/s network card – which is already quite fast – then you will need 
To counter this bottleneck is to reduce the parameters of the gradient through max pooling, maxout units or by simply using convolution. Another way is to increase the computational time/network time ratio by other means, e.g. by using is computationally intensive optimization techniques like RMSProp. You need the same time to pass the gradients to each other, but more time is spend on computation, thus increasing the utility of the fast GPUs.
Another thing you can do when you use computationally intensive optimization techniques is to hide latency of networking under the computation of the gradients. This means while you passing the first gradient to all other nodes, you can already start a big RMSProp computation asynchronously for the next layer. This technique can give a speedup of about 0-20 % depending on network architecture.
But this is not the only problem with data parallelism. There is a very technical bottleneck hidden in the GPU architecture which took me quite a while to understand. To understand why the GPU architecture is a problem we first need to look at the usage and purpose of mini-batches.
A divergence: Why do we use mini-batches?
If we start with randomly initialized parameters or even if we start with pretrained parameters, we do not need a pass through all the data to get an accurate gradient update that will head into the direction of a local minimum. If we take MNIST as an example, if we have a gradient which includes 10 common mistakes that the network does for each class (mini-batch size of about 128), then we will go into a direction that reduces the error greatly already as the gradient captures rough and common mistakes. If we choose a greater batch size (say 512) then we not only capture common errors, but also catch errors that are more subtle. However, it is not very sensible to fine-tune a system if you know it still has major errors. So overall we gain little by increasing the batch size. We need more computation to do roughly the same and this is the main argument why we use a mini-batch size as small as possible. However, if we choose a mini-batch size that is too small, then we do not capture all the common errors which are relevant for the data set and thus our gradient might not head near a local optimum, so there is a limit how small you can make mini-batches.
How does this relate to data parallelism? If we want a mini-batch size of 128 and use data parallelism to divide it among, say, eight GPUs, then each net calculates gradients for 16 samples which is then averages with the data from the other GPUs. And exactly here kicks the hardware bottleneck in.
Memory tiles: Patches of fast GPU memory for efficient dot product calculations
To calculate dot products on the GPU, you need to copy small patches, called memory tiles, into shared memory, i.e. very fast but very small memory (limited to a few kilobytes). The problem is that the standard cuBLAS uses either a 64×128 memory tiles and when you have a batch size less than 64 you waste a lot of precious shared memory. Also if you use a batch size not equal to a multiple of 32 you equally waste shared memory (threads are only started in blocks of 32 threads), so one should use a batch size which is a multiple of 32 or multiple of 64 if possible. For data parallelism this means that you lose significant processing speed once you go below a batch size of 64 for each GPU. If you have many GPUs this can be quite limiting and this is yet another reason why the data parallelism approach does not scale well beyond a certain point.
All in all this sounds quite dire for data parallelism, but data parallelism has its uses. If you know the bottlenecks, you can wield data parallelism as a might tool for certain applications. This is demonstrated by Alex Krishevsky in his paper where he uses data parallelism in the convolutional layers of his net, and thus achieves a speedup of 3.74x by using four GPUs and 6.25x using eight GPUs. His system features two CPUs and 8 GPUs in one node, so he can use the full PCIe speed for the two sets of four GPUs and relatively fast PCIe connection between CPUs to distribute the data among all eight GPUs.
Besides convolutional neural networks, another use of data parallelism might be to use it in recurrent neural networks, which typically have less parameters and highly computationally intensive gradient updates – both are wins for data parallelism.
In my next blog post I will focus on model parallelism, which is efficient for large networks and scales well to larger clusters.
Kalyan says
This part is not clear:
“Another way is to increase the computational time/network time ratio by other means, e.g. by using is computationally intensive optimization techniques like RMSProp. You need the same time to pass the gradients to each other, but more time is spend on computation, thus increasing the utility of the fast GPUs.”
Exactly how the gradients take same time to be passed to each other?
Tim Dettmers says
The idea is if you increase the time delta between computing the weight updates from one layer and the next layer, then you have more time to synchronize the weights of the next layer in backpropagation. Thus you can hide more communication under gradient computation if you use techniques which are more expensive to compute (Adam or in this case RMSProp).
Kalyan says
Got it…Thanks
Yogita says
Your blog is really useful. Your link to previous blog is unavailable. Where can I get to read that blog?
Tim Dettmers says
Thank you for pointing out that error! I correct the link’s address and it should work now.
Masoud says
Hi
Thanks for your nice explanation
Regarding to memory tiles section, I notices the same degradation when using batch size smaller than 32.
I am wondering if you have and reference that I can follow?
vinhomes riverside hai phong says
Hello there, You have done an incredible job. I will definitely digg it and personally suggest to my friends.
I’m confident they’ll be benefited from this site.
Tim Dettmers says
Thank you!
Bafu says
Hi Tim,
I like all your articles pretty much and here is a little correction for the formula calculating the time to pass a weight matrix:
passing time = weight matrix size / network bandwidth = (1000*1000*4*8) / (40*1024^3) = 0.75 (ms)
Thanks for sharing!
Justin says
Yeah, I noticed the same thing.
The equation listed in the article is incorrect, but the one Baru listed isn’t quite right either. For example, the equation in the article divides by 40 twice, which is wrong, and the last 1024 is a 102, which is also wrong. In addition, to convert from seconds to milliseconds, you have to multiply the numerator by 1000, not divide by 1000.
And as Bafu points out, you need to multiply the numerator by 8 to convert the weight matrix from bytes to bits, not divide by it. Bafu’s equation missed converting from seconds to MS which should be an additional *1000 in the numerator.
I believe the correct equation is:
(4 * 8 * 1000 * 1000 * 1000) / (40 * 1024 ^ 3)
= ~0.74ms
Séb says
I asked Tim a couple of questions per email, and here are his answers.
Q: Is it possible to use GPUDirect RDMA with Geforce cards ? (Which don’t officially support it)
A: You will be able to use GPUDirect RDMA if you have Mellanox Infiniband cards. Although it is not directly supported for GTX Titan X, it also should work there (I got it also to work for a GTX Titan, for which there is also no official support). I also heard that other people got it working with other network cards, but that probably always involves some complicated hacks.
Q: Is it worth it to go for InfiniBands instead of Ethernet for distributed deep learning ?
A: I never tested ethernet networking myself, but the stats alone speak for themselves. Especially if you want to train large convolutional networks the network bandwidth remains the main bottleneck. If your network grows larger in nodes latency will also be an issue, and as I heard ethernet latency is pretty bad. So the latency on ethernet for 8 machines might slow you down a bit (my guess would be an additional 1-10% slower or so over infiniband). If you are mainly interested to train recurrent architectures then the ethernet might be okay, since for such architectures you have much communication overhead.
Thanks again for your help,
Séb
Tim Dettmers says
Thank you for posting the Q&A here Seb! That is very helpful!
Pyry says
Thanks for the excellent posts Tim, very useful reads! We’re looking into training a large RNN language model, and are thinking of ways of parallelizing it. We have access to large numbers of free credits on AWS (also Google Cloud and Azure), and would like to train our model there.
Given this hardware constraint, any recommendations on parallelization to speed up training times? Could e.g. asynchronous updating of weights help with data parallelization, even when the network speed is not that fast? Any other ideas we should look into?
Tim Dettmers says
Parallelization of deep learning in cloud-based systems is difficult, because these systems are often optimized for regular high performance application which are not as bandwidth hungry as deep learning algorithms. If you find a cloud-service which offers InfiniBand and direct access to GPUs this could work very well. Otherwise your best bet might be to use a lot of CPU instances for the work (they do not need so much bandwidth). But it all comes down to the numbers: RNNs usually do not need so much bandwidth to begin with. Best is to take a sheet of paper and crunch the numbers: (1) How long does a forward-backward pass take? (2) How much parameters do you need to update during this time? Combining (1) and (2) will give you some bandwidth constraints (parameters in GB/s) and then you can choose your cloud-based provider accordingly. You can do this both for CPUs and GPUs and see what will work best.
For CPU based services a dedicated shard-server-system for the parameters works well; for GPUs this practice will not work well (multiple GPUs need to access the same network card for both in and out passes). I also recommend to look at parallelization papers of Google, Baidu, and Microsoft for ideas.
Hope this helps. If you need more help you are always free to ask.
Prasanna S says
Have you checked the current implementation in caffe? Recent PRs seem to have circumvented the problem in a different way. They organize the solvers in a tree in the order of speed of communication between the nodes and the final backprop is computed by the root GPU which receives the added gradient from all the children nodes. Do check them out. And NVIDIA’s Digits uses some of the PRs for multi gpu training.
Jeff says
Great article! There maybe additional tricks for this data parallel architecture. Since I/O between nodes is 3x slower than I/O between GPUs within node, you can eliminate many point-to-point comminucation by aggregating the gradients from GPUs from the same node first, and then send them over. For your configuration of 2 nodes with 3 GPUs each, you’d reduce the time from 2x (3x3xTnet + 3x2xTpcie) to 2x (2xTpcie + 2xTaggreg + Tnet). Since all I/O is RDMA, Taggreg is all Gpu time which should be very small compared to I/O. This can be significant savings. If you further interleave the Tnet with Tpcie and Taggreg, you can probably synchronize all within 2xTnet (amortized).
Jeff says
Oops, the above formula should read 2x (2x Tpcie + Taggreg + Tnet + Taggreg + 2xTpcie). I forgot the time to distribute the result to the ither 2GPUs after the final aggregation. But the reasoning still holds.
timdettmers says
Thanks for your comment Jeff – very sound logic! In fact I thought of this too, but I could not get it working better than straightforward GPU to GPU communication. I do not know why this is exactly so, but as far as I could understand it was probably a factor of two things: (1) One has a step by step procedure where every aggregation needs to be completed before you can proceed to the next step, this is also true when one writes the results back to the 2 other GPUs; (2) you will have extra compute time to aggregate the gradients in the “master GPU” of each node.
For (2) my implementation was naive, where I added all gradients together. I think I could have improved (2) by adding the gradients asynchronously by using streams. It might well be that my implementation for (1) was not optimal (cudaStreamSynchronize() after the kernel followed by MPI communication; and MPI_Wait() followed by MPI communication). I think one can make this procedure actually work, but it just requires some additional work.